Histograms: Base graphics
- The workhorse function is
hist
Lauren Talluto
13.01.2025
R is two things:
RStudio is a comprehensive working environment for R
(https://rstudio.com/products/rstudio/)
Any code that is given to you will assume your working directory is
set to the unit you are working on. So, for today’s
exercises, you should run the following in the console:
setwd("unit_1").
# character is a comment and
will be ignored by the interpreter._ symbol.= or <- symbol= or
<-, not both)# Comments in R start with the # symbol
# anything after # will not be executed
# Comments are a useful way to annotate your code so you know what is
# happening
# Legal variable names
x = 1
y0 = 5
time_of_day = "20:15"
dayOfWeek <- "Monday"
# bad!
# d is the diversity in our site, in species
d = 8
# better!
site_diversity = 8
# errors
0y = 5
my name = "Lauren"
## Error: <text>:21:2: unexpected symbol
## 20: # errors
## 21: 0y
## ^numeric: integers and floating-point (decimal)
numberslogical: yes/no, true/false data; in R represented by
the special values TRUE and FALSE
T and F (no quotes) can be used as
shortcuts for TRUE/FALSE, but you should avoid
this!character: strings, textfactor: special variable type for categorical (nominal
& ordinal) dataWe use operators to perform computations on variables and constants
=, <-+, -, *,
/, ^, %%==, !=, <,
>, <=, >=&), or
(|), and not (!).&), or
(|), and not (!).Mathematical functions
sin(), cos()log(), exp(), sqrt()Get help on a function with ? or help(),
for example: ?log or help(log). If you don´t
know a function´s name, you can search for a (likely/suspected) string
in its name with ??.
x = 5
# The print() function takes one or more arguments
#. in this case the variable x
# It returns no value, but has the side effect of printing the
# value of x to the screen
print(x)
## [1] 5vector holds one or more values of a single data type
c()# The c() function stands for concatenate
# it groups items together into a vector
(five_numbers = c(3, 2, 8.6, 4, 9.75))
## [1] 3.00 2.00 8.60 4.00 9.75vector holds one or more values of a single data type
c()[]vector holds one or more values of a single data type
c()[]data.frame holds tabular data
row of a data frame is a single
case (i.e., an observation)column of a data frame is a single variable (i.e.,
a vector, all the same data type)head shows the first few rows of a data frame# Load a dataset named 'penguins' and
# convert it to a data frame
# this dataset comes from a package, "palmerpenguins"
data(penguins, package = "palmerpenguins")
penguins = as.data.frame(penguins)
head(penguins)| species | island | bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | sex | year |
|---|---|---|---|---|---|---|---|
| Adelie | Torgersen | 39.1 | 18.7 | 181 | 3750 | male | 2007 |
| Adelie | Torgersen | 39.5 | 17.4 | 186 | 3800 | female | 2007 |
| Adelie | Torgersen | 40.3 | 18.0 | 195 | 3250 | female | 2007 |
| Adelie | Torgersen | NA | NA | NA | NA | NA | 2007 |
| Adelie | Torgersen | 36.7 | 19.3 | 193 | 3450 | female | 2007 |
| Adelie | Torgersen | 39.3 | 20.6 | 190 | 3650 | male | 2007 |
View shows the data frame in a graphical windowstr gives you a summary of the
structure of the datastr(penguins)
## 'data.frame': 344 obs. of 8 variables:
## $ species : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ island : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ bill_length_mm : num 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42 ...
## $ bill_depth_mm : num 18.7 17.4 18 NA 19.3 20.6 17.8 19.6 18.1 20.2 ...
## $ flipper_length_mm: int 181 186 195 NA 193 190 181 195 193 190 ...
## $ body_mass_g : int 3750 3800 3250 NA 3450 3650 3625 4675 3475 4250 ...
## $ sex : Factor w/ 2 levels "female","male": 2 1 1 NA 1 2 1 2 NA NA ...
## $ year : int 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...nrow, ncol, dim give you
dimensions of the data frame$ or
[]# accessing a variable by name
penguins$bill_length_mm
# accessing a variable by position
penguins[,1] # [,1] get every row in the first column# accessing a variable by name, and subsetting rows
penguins[1:10,"bill_length_mm"] # another way to access by name, gets the first 10 entries
## [1] 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42.0$bill_length_mm, [,1],
[, 'bill_length_mm']).complete.cases, which returns the rown
numbers of all rows that do not contain any NAs.The variable species is a factor, representing a
categorical variable with a fixed set of levels.
str(penguins)
## 'data.frame': 333 obs. of 8 variables:
## $ species : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ island : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ bill_length_mm : num 39.1 39.5 40.3 36.7 39.3 38.9 39.2 41.1 38.6 34.6 ...
## $ bill_depth_mm : num 18.7 17.4 18 19.3 20.6 17.8 19.6 17.6 21.2 21.1 ...
## $ flipper_length_mm: int 181 186 195 193 190 181 195 182 191 198 ...
## $ body_mass_g : int 3750 3800 3250 3450 3650 3625 4675 3200 3800 4400 ...
## $ sex : Factor w/ 2 levels "female","male": 2 1 1 1 2 1 2 1 2 2 ...
## $ year : int 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...Useful functions for factors include levels and
table.
R currently has two dominant graphical engines
hist
histThe defaults are not very nice, so lets improve things
main = "" disables the titlexlab and ylab control axis labelsbreaks controls the number of bins in the
histogramcol sets the color of the barsborder sets the color of the borders (NA:
no border)
#RRGGBB
00 (none) to FF
(most)col = rosybrowncolors() function for the names



The population mean (\(\mu\)) can be approximated with the sample mean:
\[ \mu \approx \bar{x} = \frac{1}{n}\sum_{i=1}^n x_i \]
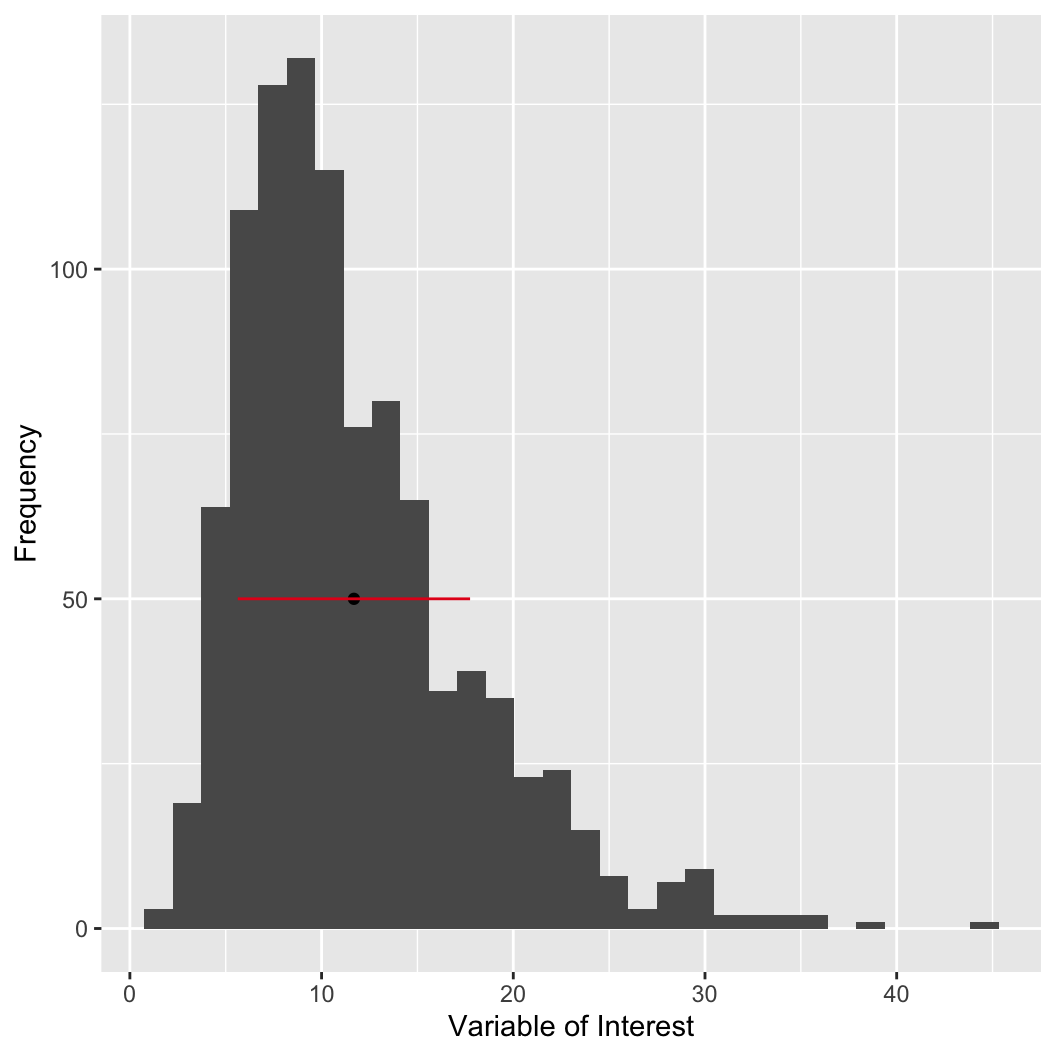
The mean can be strongly influenced by outliers.
The mean can be strongly influenced by outliers.
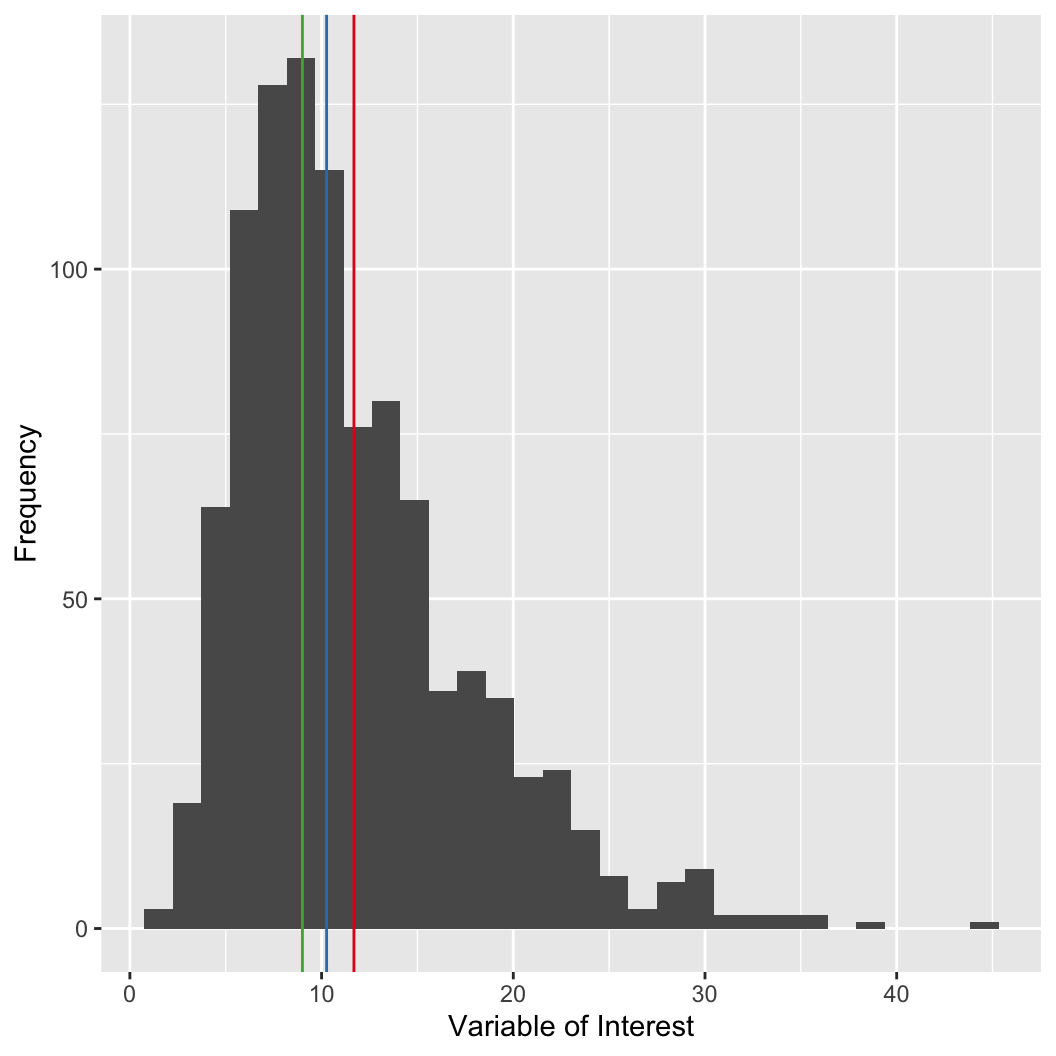
The mean can be strongly influenced by outliers.
hist!
# we can use the histogram function to approximate the sample mode
# WARNING: changing the number of breaks can have a
# large impact on the results
my_hist = hist(my_var, breaks = 30, plot = FALSE)
# the mids variable gives you the midpoint of each bin
# counts gives you the count each bin
# cbind shows them together in columns
cbind(bar_midpoint = my_hist$mids, count = my_hist$counts)
## bar_midpoint count
## [1,] 1 2
## [2,] 3 31
## [3,] 5 116
## [4,] 7 161
## [5,] 9 170
## [6,] 11 147
## [7,] 13 92
## [8,] 15 84
## [9,] 17 48
## [10,] 19 50
## [11,] 21 31
## [12,] 23 24
## [13,] 25 15
## [14,] 27 5
## [15,] 29 10
## [16,] 31 6
## [17,] 33 2
## [18,] 35 4
## [19,] 37 0
## [20,] 39 1
## [21,] 41 0
## [22,] 43 0
## [23,] 45 1The mean can be strongly influenced by outliers.
hist!We can compare variables in a way that is location independent by centering (subtracting the mean)
\[ \sigma^2 = \frac{1}{N}\sum_{i=1}^N (X_i-\mu)^2 \]
We can estimate \(\sigma^2\) using the sample variance:
\[ \sigma^2 \approx s^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i -\bar{x})^2 \]
It is convenient to talk about the scale of \(x\) in the same units as \(x\) itself, so we use the (population or sample) standard deviation:
\[ \sigma = \sqrt{\sigma^2} \approx s = \sqrt{s^2} \]
\[ \sigma^2 = \frac{1}{N}\sum_{i=1}^N (X_i-\mu)^2 \]
We can estimate \(\sigma^2\) using the sample variance:
\[ \sigma^2 \approx s^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i -\bar{x})^2 \]
It is convenient to talk about the scale of \(x\) in the same units as \(x\) itself, so we use the (population or sample) standard deviation:
\[ \sigma = \sqrt{\sigma^2} \approx s = \sqrt{s^2} \]
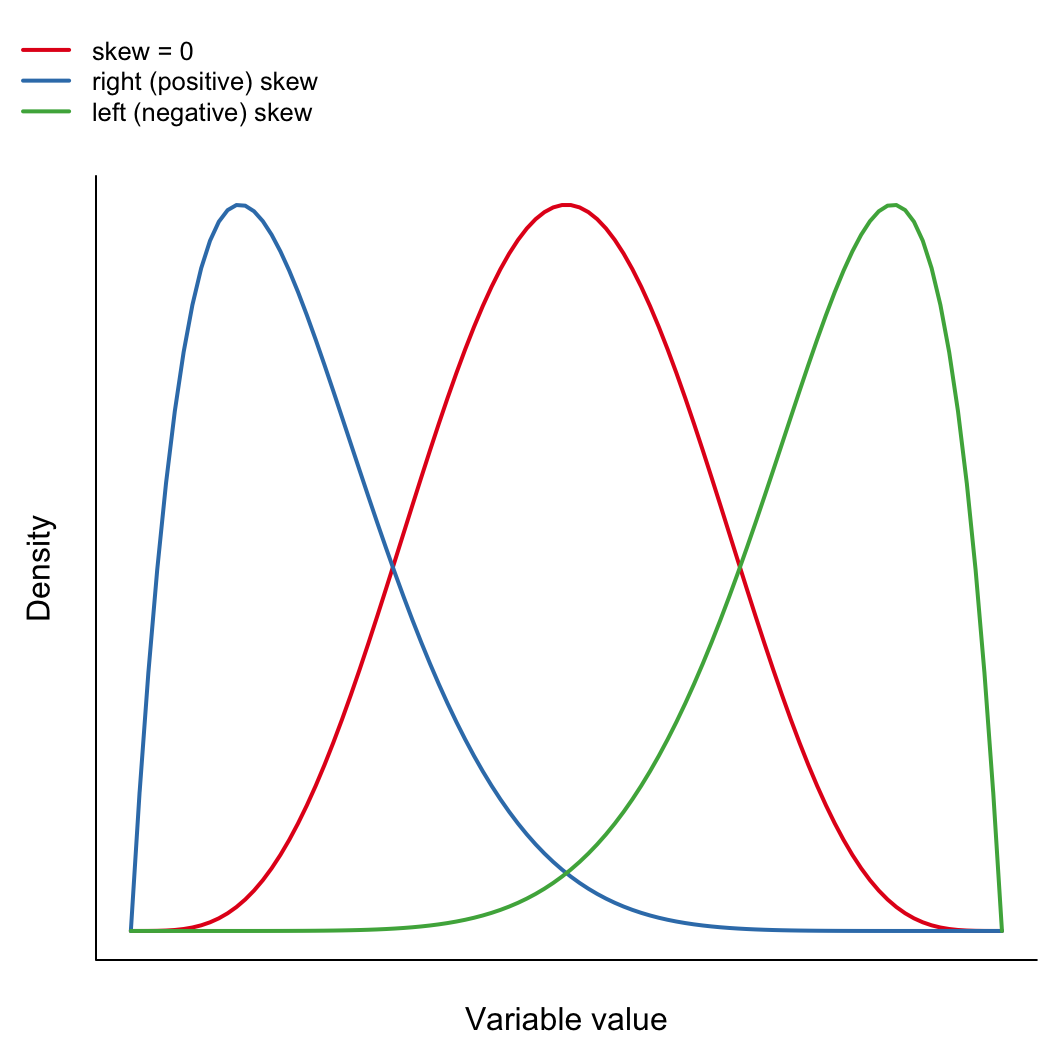
max(x) - min(x)Is the distribution weighted to one side or the other?
\[ \mathrm{skewness} = \frac{\sum_{i=1}^{n}(x_i-\bar{x})^3}{(n-1)s^3} \]
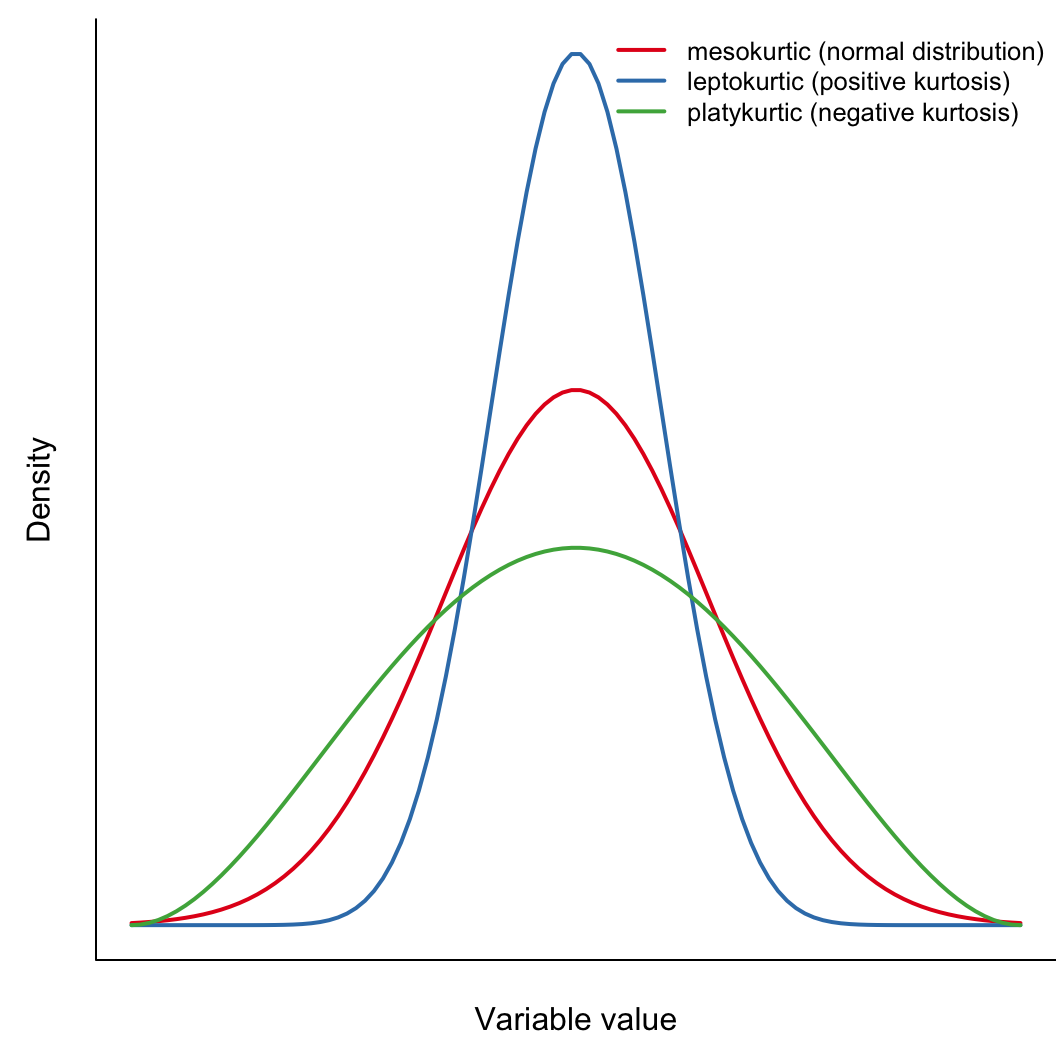
How fat are the tails relative to a normal distribution?
\[ \mathrm{kurtosis} = \frac{\sum_{i=1}^{n}(x_i-\bar{x})^4}{(n-1)s^4} \]
boxplot functiony ~ group is a special data type called a
formulaboxplot functiony ~ group is a special data type called a
formulaboxplot functiony ~ group is a special data type called a
formulaFor more complex groupings, better to use ggplot
penguins datasetmean separately to every variable in
penguinssimple apply (sapply)# bad!
(col_means = c(
mean(penguins[,3]),
mean(penguins[,4]),
mean(penguins[,5]),
mean(penguins[,3]) # it's easy to introduce mistakes this way!
))
## [1] 43.99279 17.16486 200.96697 43.99279
# better
# first we find out which columns are numeric
numeric_columns = sapply(penguins, is.numeric)
# then we get the means of those columns
(col_means = sapply(penguins[,numeric_columns], mean))
## bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
## 43.99279 17.16486 200.96697 4207.05706
## year
## 2008.04204mean separately to every variable in
penguinssimple apply (sapply)sapply(penguins[,numeric_columns], range)
## bill_length_mm bill_depth_mm flipper_length_mm body_mass_g year
## [1,] 32.1 13.1 172 2700 2007
## [2,] 59.6 21.5 231 6300 2009# here, we pass an additional argument named probs to quantile
# see ?quantile for what this does
sapply(penguins[,numeric_columns], quantile, probs = c(0.25, 0.5, 0.75))
## bill_length_mm bill_depth_mm flipper_length_mm body_mass_g year
## 25% 39.5 15.6 190 3550 2007
## 50% 44.5 17.3 197 4050 2008
## 75% 48.6 18.7 213 4775 2009tapply: tabular apply
bill_length_mm) based on categories in another variable
(e.g., species)
Thought experiment
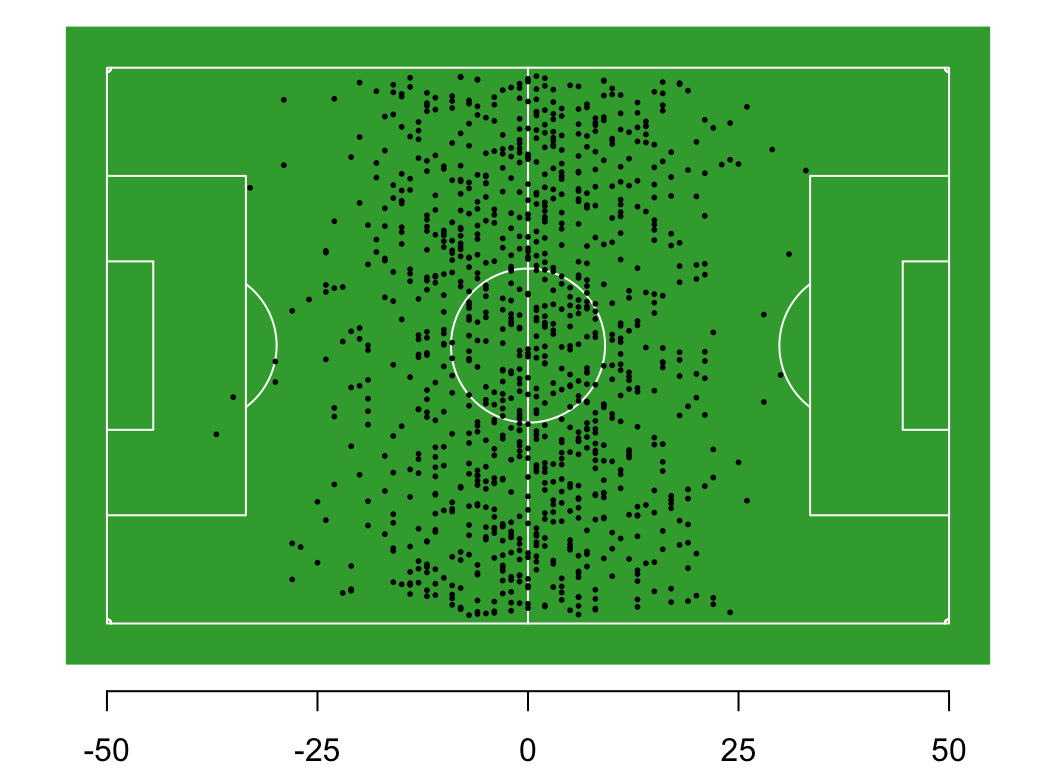
You and 99 of your closest friends gather on the centre line of a 100-m football pitch. We define the centre line as 0m, the western boundary -50 m, and the eastern boundary as +50 m.
Thought experiment
You and 99 of your closest friends gather on the centre line of a 100-m football pitch. We define the centre line as 0m, the western boundary -50 m, and the eastern boundary as +50 m.
Each person flips a coin. If the coin is heads, they take a step east (add 0.5 m to their location), if its tails, they take a step west (subtract 0.5 m from their location).
Question: What is the long-run distribution of positions on the field?
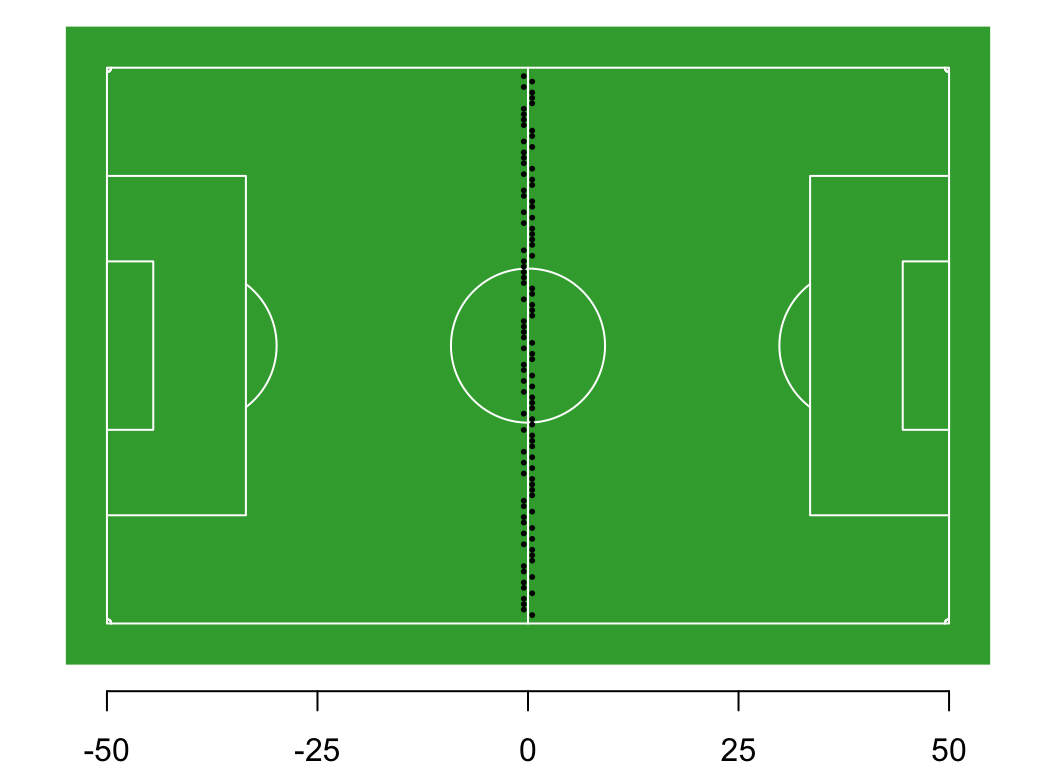
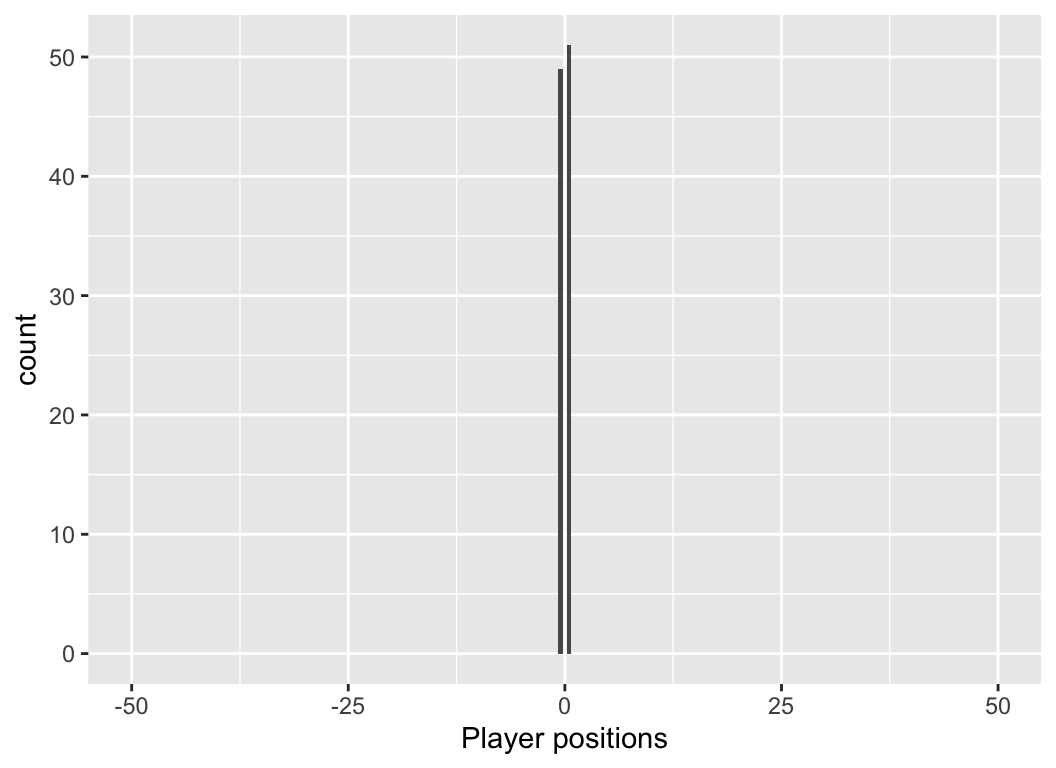
Thought experiment
You and 99 of your closest friends gather on the centre line of a 100-m football pitch. We define the centre line as 0m, the western boundary -50 m, and the eastern boundary as +50 m.
Each person flips a coin. If the coin is heads, they take a step east (add 0.5 m to their location), if its tails, they take a step west (subtract 0.5 m from their location).
Question: What is the long-run distribution of positions on the field?
Exercise: Try to simulate this process in R. What does the distribution of locations look like after 10 steps? After 100? What is the long-run distribution with many steps and many players?
# if you want to draw the soccer pitch, you can read the function for it
source("r/football.r")
# 100 players, all on the centre line (value = 0)
nplayers = 100
players = rep(0, nplayers)
# define the size of the steps for each coin flip
heads = 0.5
tails = -0.5
# simulate one step for each player
steps = sample(c(heads, tails), nplayers, replace = TRUE)
# update player locations
players = players + steps
# visualise, if desired
draw_pitch(players)
hist(players)Thought experiment
You and 99 of your closest friends gather on the centre line of a 100-m football pitch. We define the centre line as 0m, the western boundary -50 m, and the eastern boundary as +50 m.
Each person flips a coin. If the coin is heads, they take a step east (add 0.5 m to their location), if its tails, they take a step west (subtract 0.5 m from their location).
Question: What is the long-run distribution of positions on the field?
Exercise: Try to simulate this process in R. What does the distribution of locations look like after 10 steps? After 100? What is the long-run distribution with many steps and many players?
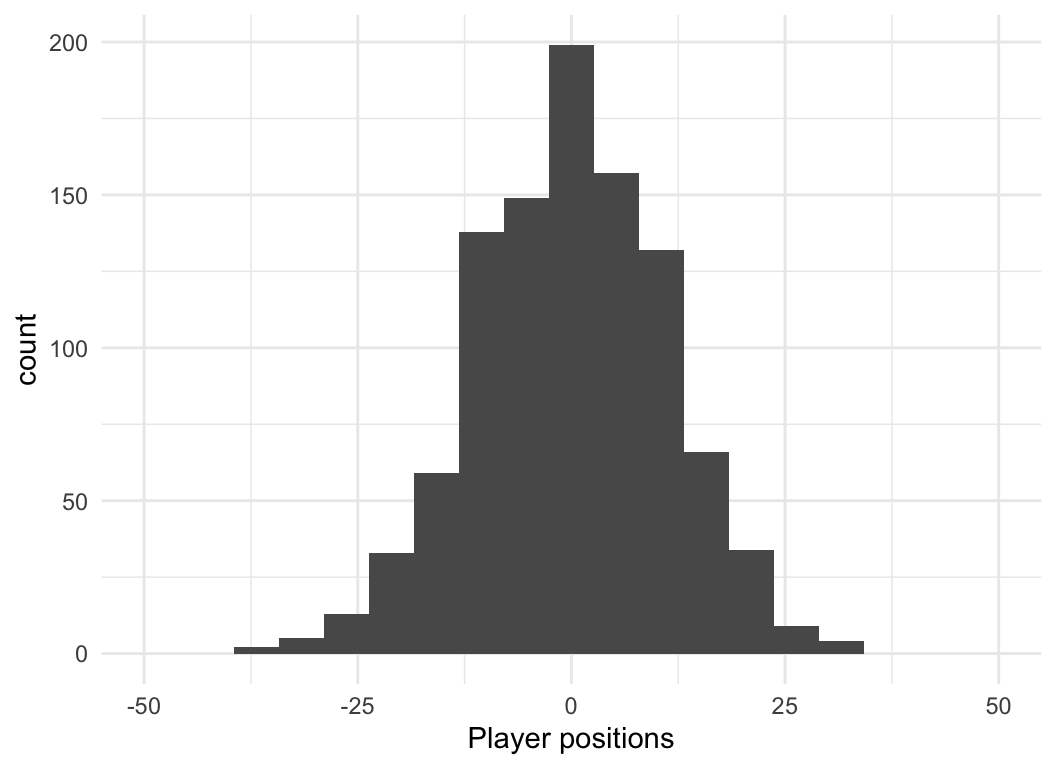
density function in R to add a curve
approximating this density.hist(players, breaks=40, col="gray", main = "", freq=FALSE)
lines(density(players, adjust=1.5), col='red', lwd=2)
mu = mean(players)
sig = sd(players)
x_norm = seq(min(players), max(players), length.out = 400)
y_norm = dnorm(x_norm, mu, sig)
lines(x_norm, y_norm, lwd=2, col='blue')
legend("topright", legend=c(paste("sample mean =", round(mu, 2)),
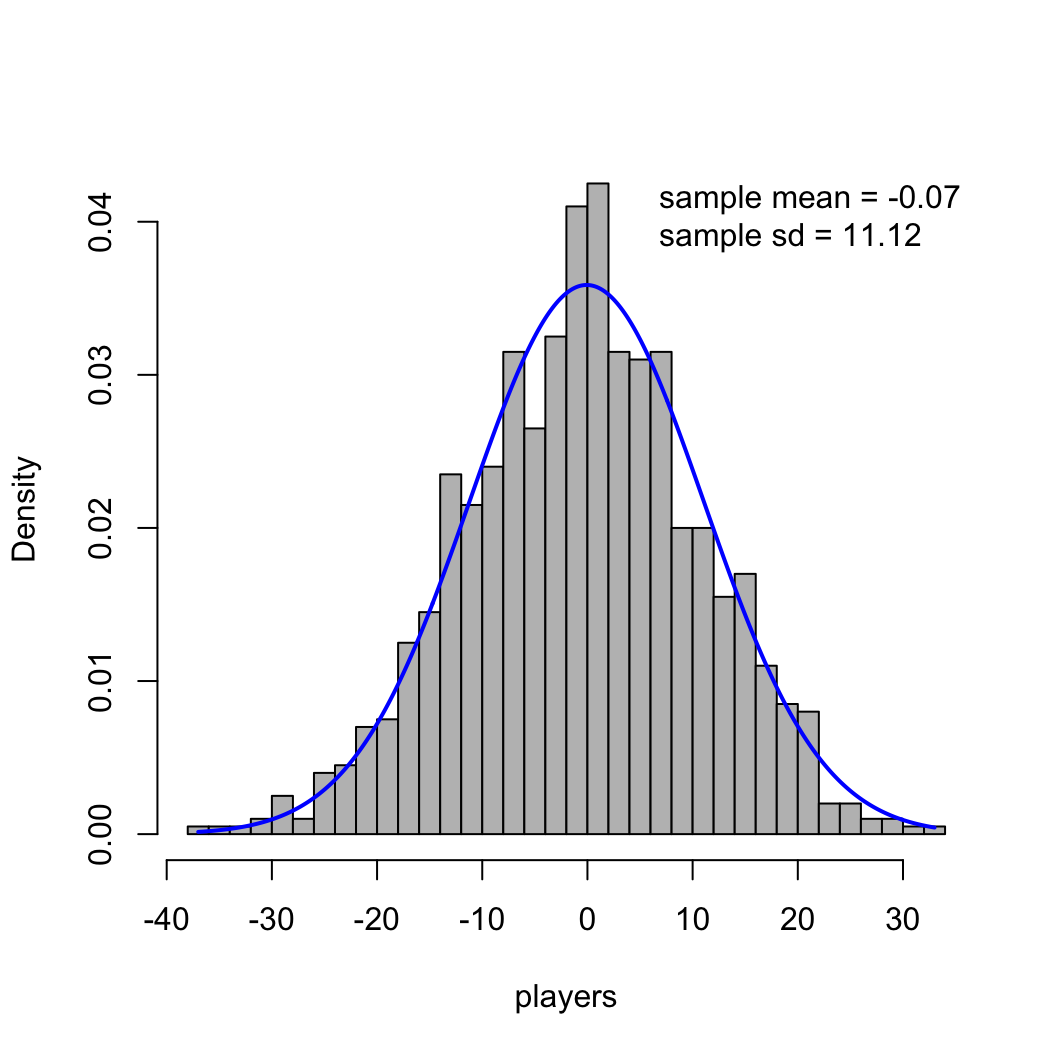
paste("sample sd =", round(sig, 2))), lwd=0, bty='n')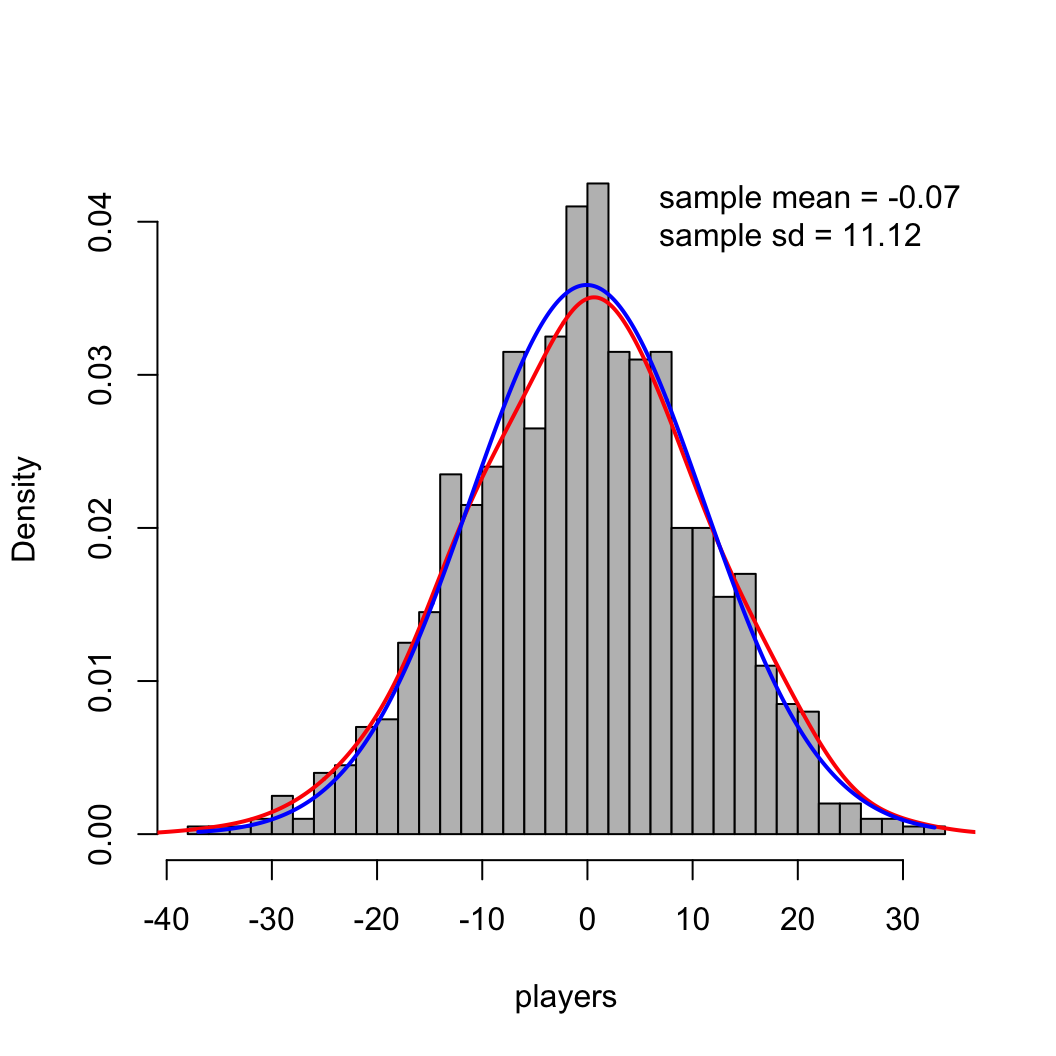
scale function.\[ \mathcal{f}(x) = \frac{1}{\sigma \sqrt{2\pi}} \mathcal{e}^{-\frac{1}{2} \left (\frac{x-\mu}{\sigma} \right )^2} \]
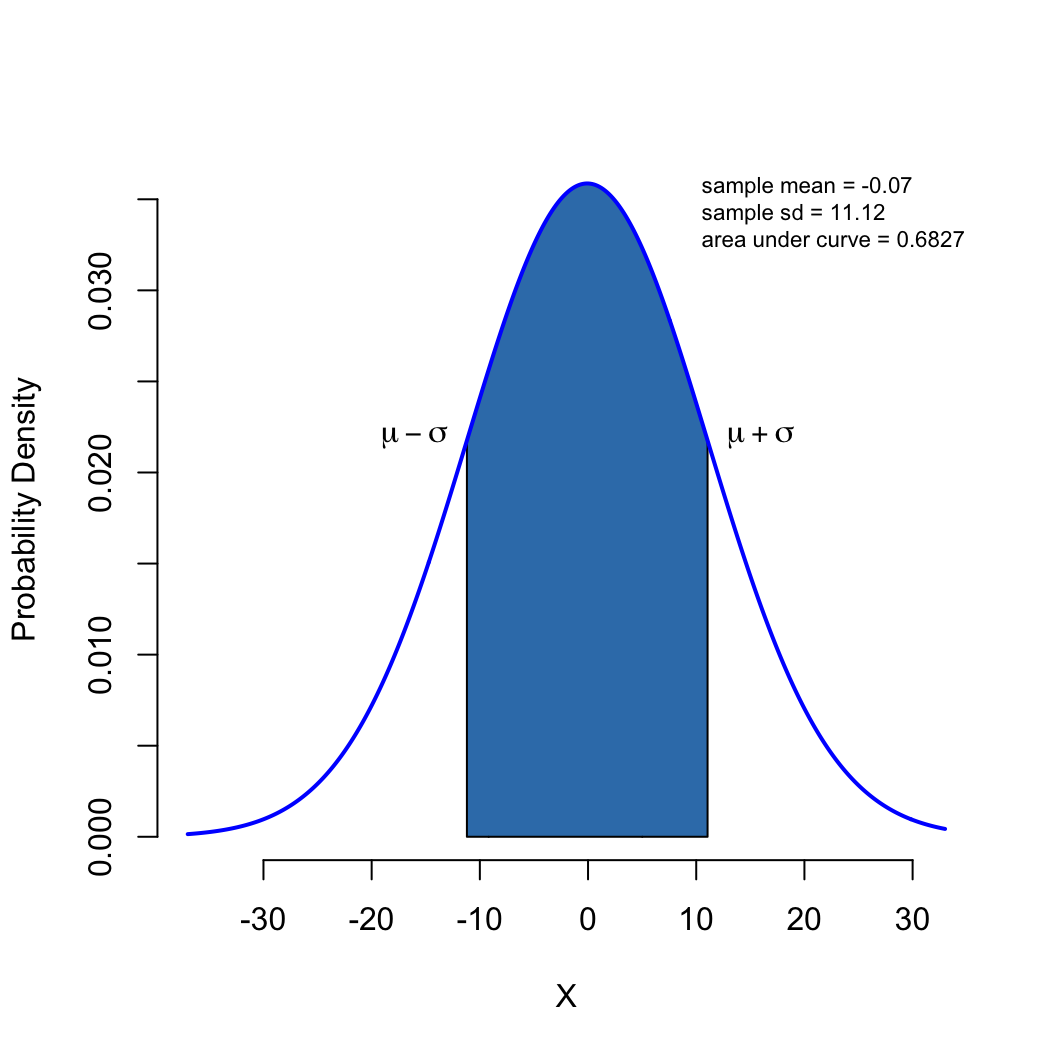
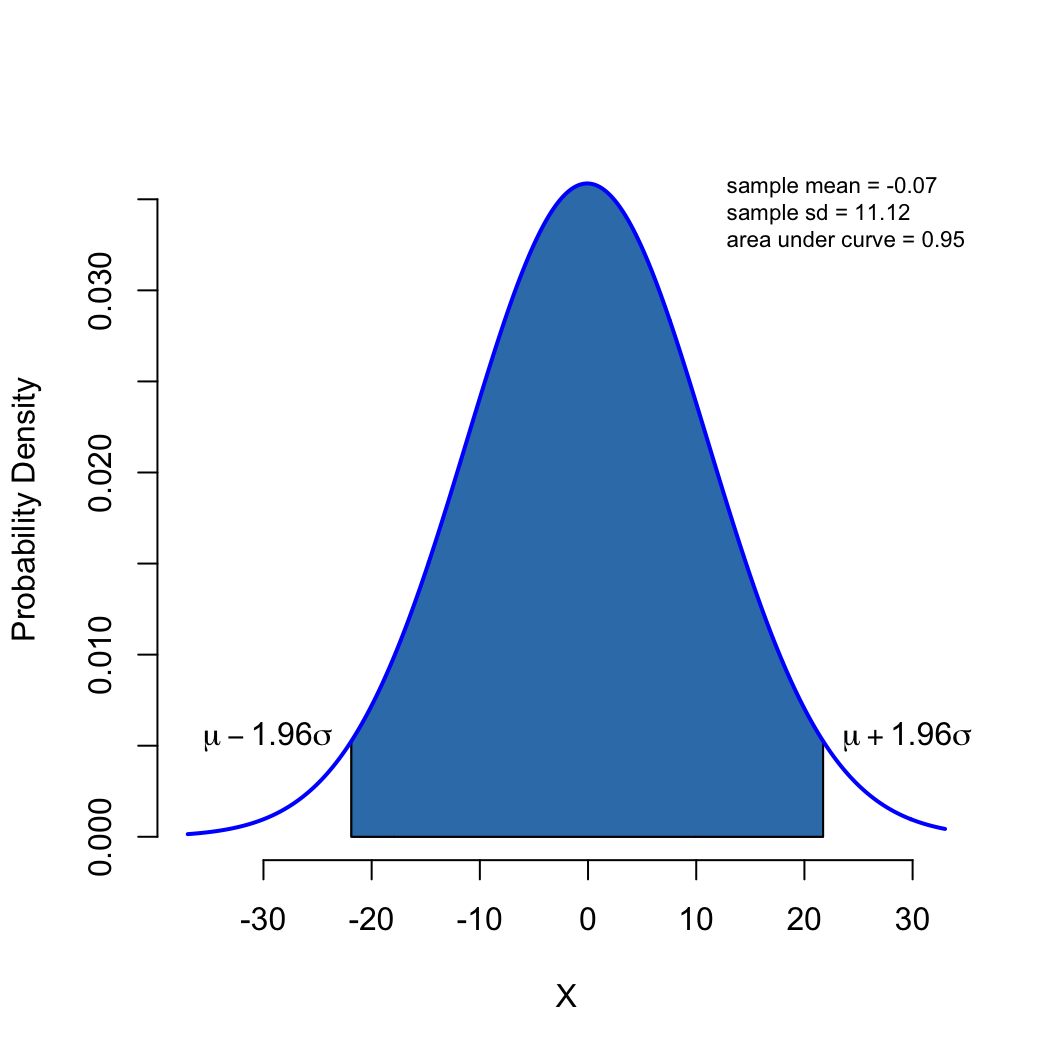
\[ \mathcal{g}(x) = \int_{-\infty}^{x} \frac{1}{\sigma \sqrt{2\pi}} \mathcal{e}^{-\frac{1}{2} \left (\frac{x-\mu}{\sigma} \right )^2} dx \]
PDF: what is the probability density
when \(x=3\) (the height of the bell
curve)
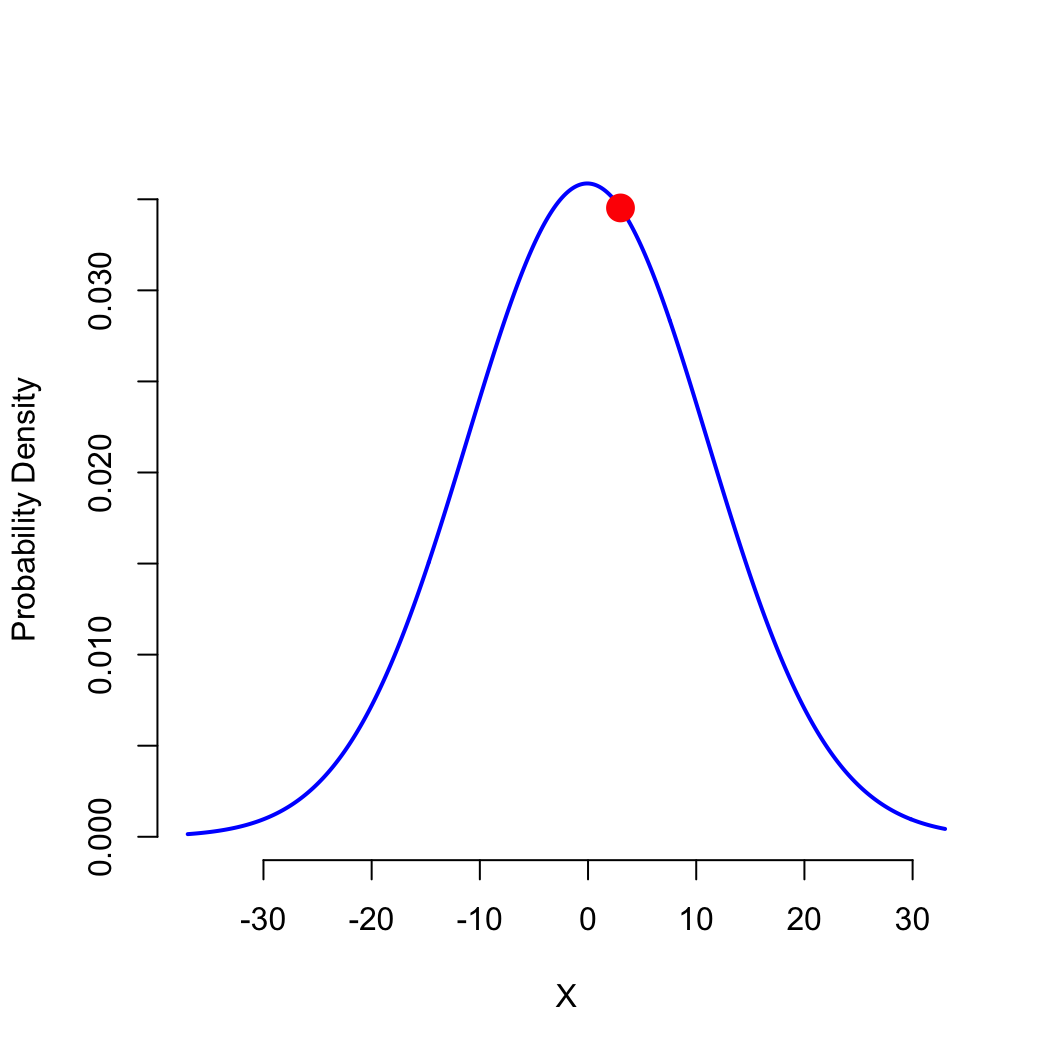
PDF: what is the probability density
when \(x=3\) (the height of the bell
curve)
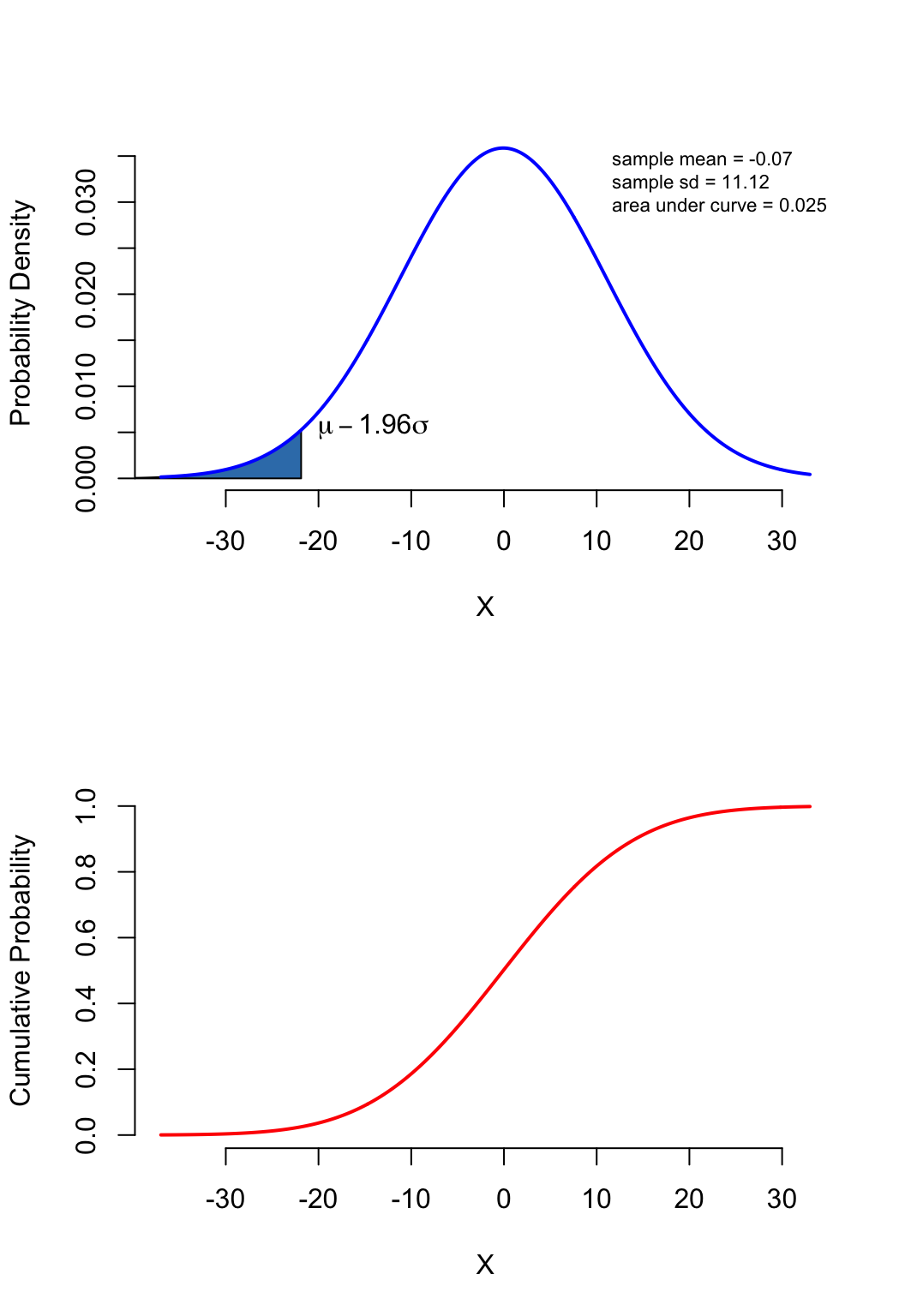
CDF: what is the cumulative probability
when \(x=q\)
(area under the bell curve from \(-\infty\) to \(q\))
(probability of observing a value < \(q\))
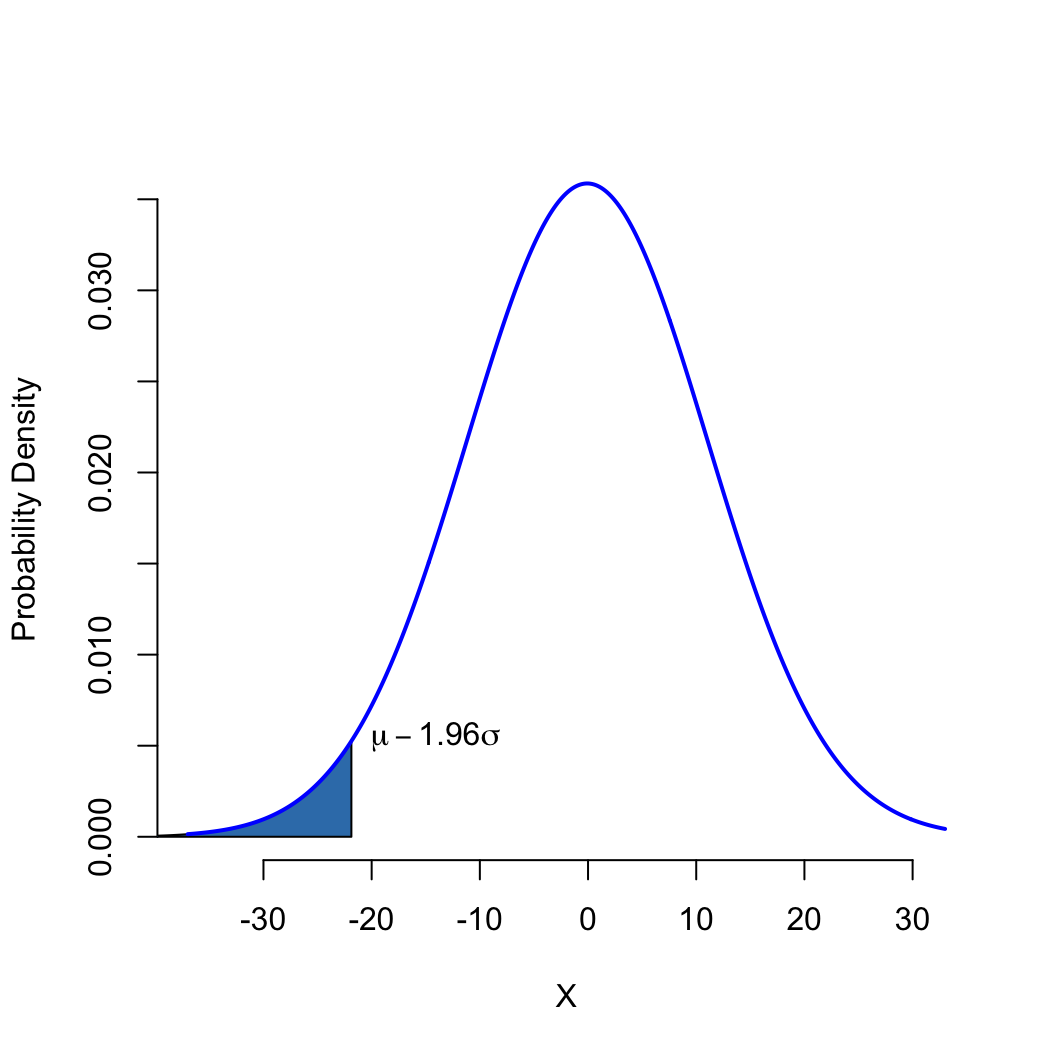
Quantiles: what is the value of \(x\), such that the probability of observing x or smaller is \(p\)
(inverse of the CDF/pnorm)
Quantiles: what is the value of \(x\), such that the probability of observing x or smaller is \(p\)
(inverse of the CDF/pnorm)
RNG: Random number generator, produces \(n\) random numbers from the desired distribution
\[ \sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}} \approx \frac{s}{\sqrt{n}} \]